Orbital Mechanics - Hohmann Interplanetary Trajectories and Gravity Assists
Neighborly Rendezvous
Traveling to other planets is just like rendezvousing with another spacecraft in a different orbit, because that is exactly what you are doing. The interplanetary spacecraft is moving from Earth’s orbit to, say, Mars’ orbit, to rendezvous with the red planet. In traveling to Mars, the spacecraft is moving to a higher orbit. Remember from Orbital Mechanics part 1, to raise the apogee of an orbit, we fire the engines at perigee. On a Mars mission, Earth orbit is the perigee—but since we are leaving the home planet and moving into solar space, it is now called perihelion. Mars’ orbit is aphelion. A Hohmann Transfer Orbit trajectory does the job nicely, with the engines fired in the direction of Earth’s movement in it’s’ orbit.
Of course, there are some differences. The spacecraft must be accelerated to about 25,000 mph to escape Earth’s gravity. It must start its journey at a time that will allow it to cross Mars’ orbit when the red planet is at that same point in its orbit. And it should be moving in the same direction Mars is moving. That requires some serious orbital calculations.
Once the spacecraft arrives at Mars, it must fire its rockets to slow itself sufficiently to go into orbit around the fourth planet. Even most landers first achieve a ‘parking’ orbit before making their descent to the surface.
But, suppose we want to travel to the second planet in the solar system—Venus? The Hohmann Transfer maneuver still applies, as does the need to achieve escape velocity. Remember from Part 1, to lower the apogee the engines must be fired opposite to the direction of travel. Since the Earth’s orbit is at aphelion and Venus’ at perihelion, the engines are fired opposite to the direction of Earth’s motion so the spacecraft falls toward the sun.
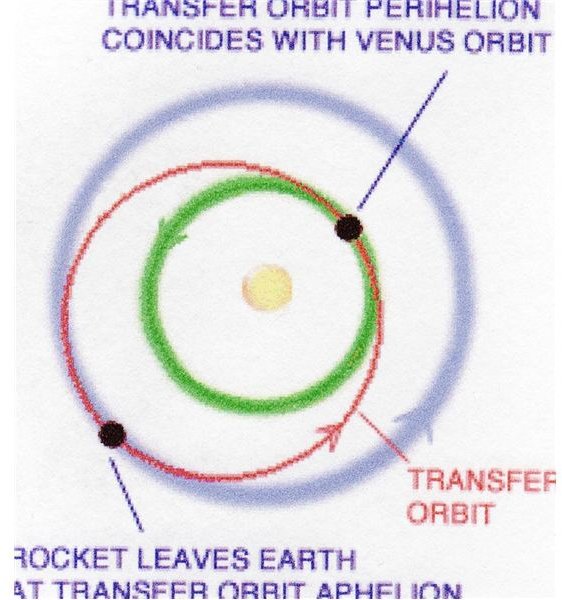
A Natural Assist
With today’s rockets, even using LH2, the energy requirements for reaching planets beyond Mars and Venus are at best at the edge of their potential. To get to the outer planets, rocket scientists have had to take advantage of nature’s own energy store—gravity.
Mars is a ‘mere’ 35 million miles away at closest approach. A low energy Hohmann trajectory can take a spacecraft there easily. Jupiter, the next planet in the solar system, is 365 million miles distant at its closest approach. Even the giant SATURN V could not send a spacecraft of any significant size that far.
But gravity can.
Let’s say we launch a spacecraft towards Mars, but not to orbit or land on it—to use its gravitational pull to speed the spacecraft up to a velocity that will allow it to continue on to Jupiter. This is known as a gravity assist.
As the spacecraft approaches Mars, that planet’s gravitational field pulls it ever faster towards it. As we approach the planet we begin to also pick up its angular momentum. This gives the spacecraft sufficient velocity to exit the planet’s gravity well without being slowed. It whizzes past the helping world with more velocity and on a different trajectory, which, if we’ve done our calculations correctly, will take it to Jupiter
And think where we could go if we used massive Jupiter to sling shot our way out into the solar system. That’s exactly what NASA did with Pioneer and Voyager. Both used Jupiter’s gravity assist to send them on to Saturn, and in Voyager’s case to Neptune and Uranus.
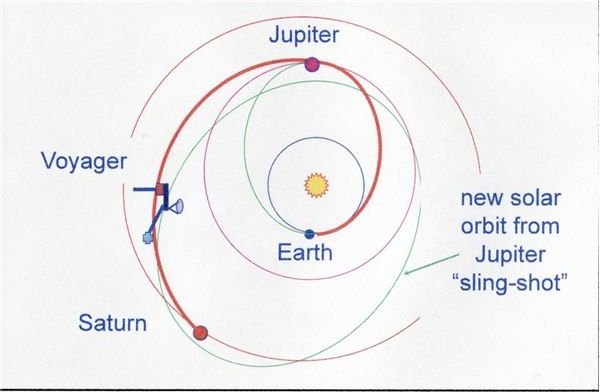
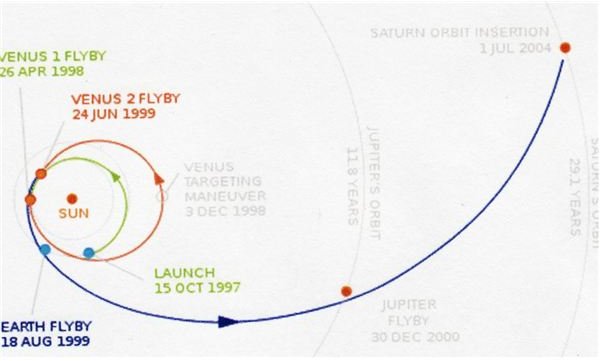
The Cassini spacecraft used Jupiter’s gravity assist. But not just that giant. Cassini first flew to Venus, whipped around it, came back to Earth’s orbit, went back to Venus, picked up more speed, flew back to Earth to gain more velocity, and headed to Jupiter. Jupiter’s huge gravity field sped the craft up more and sent it on the Saturn, where it remains in orbit today, still sending pictures of that giant and its’ moons. At one point in Cassini’s flight, it was travelling more than 28,600 mph.

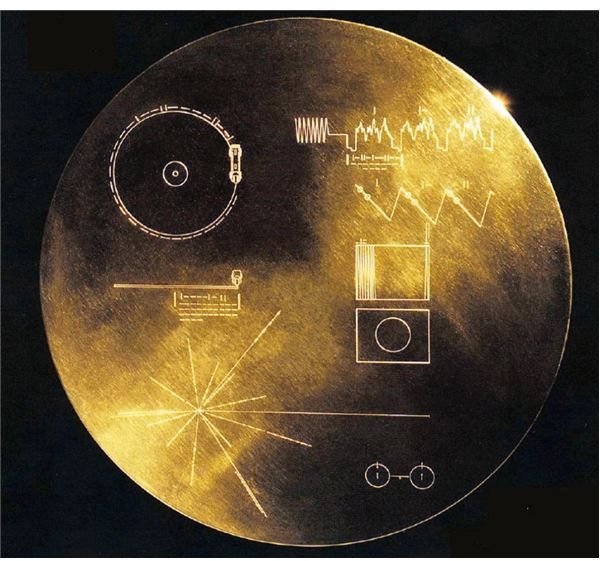
Voyager 2, one of our first interplanetary probes, today has left the solar system with the speed it obtained from the gravity assist it received from Uranus. It is drifting in interstellar space. On its side is a plaque containing symbols we hope some spacefaring species or future humans can decipher. Inside the plaque is a video disc containing music and greetings in many languages.
Perhaps in some distant future, astronauts from a planet orbiting a distant star will find our celestial message in a bottle, calculate where it came from, and come to visit…
More Free Energy
Around every celestial body orbiting a star or a planet, there are certain points at which the two gravitational fields create a balance between the two. At these points, other masses, such as asteroids, often congregate because the gravitational fields are evenly balanced. An example are the Trojan asteroids in Jupiter’s orbit.
These points are called LaGrange points after French mathmetician Joseph LaGrange, who discovered them. There are five such points in any two body system, but they are more distinct when one body is much more massive than the other. In the Earth/Sun system—and other planets—there are five LaGrange points, designated L1,L2…L5. As you can see from the illustration, L1 and L2 are close to the Earth, or the less massive body. L3 is on the opposite side of the orbit. L4 and L5 are at 60 degree angles to the more massive body, in the orbit of the smaller body. These are the Trojan points.
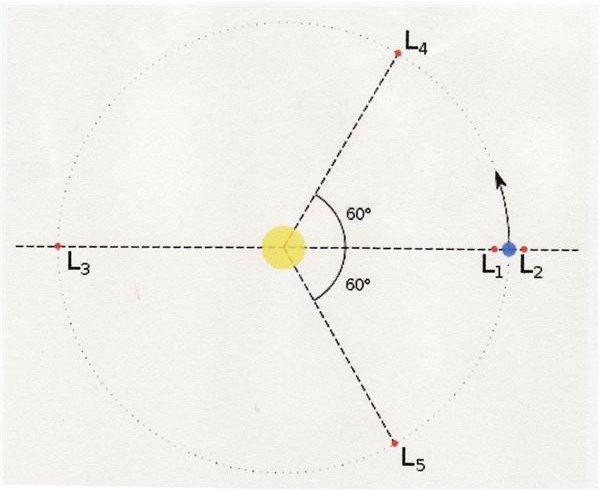
Because the LaGrange points are points where the gravitational fields of the two bodies are exactly balanced, a third body at one of these points, particularly L1 or L2, is precariously balanced. It is as if you tried to balance a ball on the tip of a pyramid. You might get it to stay, but the slightest nudge will cause it to fall off. So, too, a spacecraft at L1 or L2. With just the least bit of push towards one of the two bodies, it will move toward that body and begin to pick up speed. In the 1960s, mathematicians Charles Conley and Richard McGhehee developed the concept that this phenomenon could be used to propel a spacecraft away from Earth with very little or NO energy expenditure. Further work showed that this capability could connect LaGrange points throughout the Solar System if the proper trajectory and timing were chosen.
In other words, using the LaGrange phenomenon, spacecraft could fly from Earth to say Jupiter with much less energy expenditure than even with Hohmann transfers and gravity assists. This method of spaceflight became known as the Interplanetary Transportation Network (ITN) or the Interplanetary Superhighway. In the illustration, the ‘highways’ are depicted as tubes, because the math treats them as such. The green ribbon represents just one path among many contained within the bonding tube.

And, this isn’t just theory. It has been used for several space missions, including NASA’s Genesis, which is collecting solar wind particles. Japan used the ITN for their moon probe.
But, there is a down side to the ITN. It saves propellant, but it is even slower than Hohmann trajectories and gravity assist routes. Cassini took five years to reach Saturn with its convoluted journey. Using the ITN would take decades.
Interplanetary Speedsters
What is needed is an engine that can continually accelerate a spacecraft on its journey, so the craft keeps gaining velocity, rather than losing it to the pull of gravitational forces. One that does that is flying now, and a more powerful one is being tested.
An ion engine propelled Deep Space 1 (DS1) to a rendezvous with Comet Borelly in 2001, and another ion engine is speeding the DAWN spacecraft to the asteroid belt for close encounters with three asteroids.
An ion engine relies not on exhausting tons of propellant to produce acceleration, but on mere ounces. This means the thrust of an ion engine is very low—also mere ounces. DS1’s engines produced 0.02 lbs of thrust. But it makes up for that with an incredibly high exhaust velocity—in the case of the DS1 and DAWN engines, 25 miles per second. Theoretically, an ion engine’s Ev is unlimited, determined only by the amount of electrical power used to generate the ions.

An ion engine uses xenon as fuel. This is stripped of its electrons by a high electric charge to create ions. The ions are then accelerated by an electric field as exhaust to propel the spacecraft.
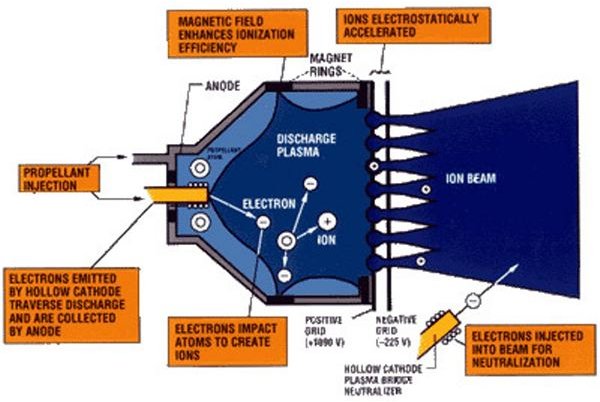
The ion engine can operate continuously, giving the spacecraft ever increasing speed, albeit at small increments. DS1’s engines increased its speed by 7900 mph over its flight time. DAWN’s engines will run for 5000 hours.
The other type engine now being developed is a plasma engine. In this device, a fuel, usually hydrogen, is ionized. Very high frequency radio waves then heat it to extreme temperature to create plasma. Magnetic fields contain the plasma within the engine and direct it out the nozzle to produce low levels of thrust.
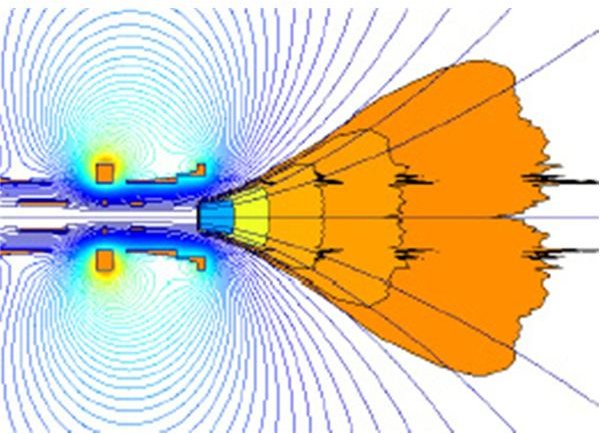
NASA’s plasma engine, VASIMR, will be tested on the ISS in 2011. VASIMR has the unique capabilty of having variable thrust, though still of very low levels.
A recent study at Georgia Tech showed that a variable thrust type engine similar to VASIMR, with its thrust properly directed, could cut the transit time to Venus from the current nine months to one month.
This post is part of the series: Orbital Mechanics and Interplanetary Trajectories
Flying is space requires a completely different way of thinking. You don’t simply move in a straight line from one point to another. You are always moving in an ellipse as a result of gravitational forces from the planet or the sun in the case of interplanetary flight. That is different.
