The Hardy-Weinberg Equilibrium Theorem in Population Genetics
Suppose you have an infinitely large population with one gene that has two alleles. Call the alleles A and a. Both alleles are equally good in terms of evolutionary fitness (so, no natural selection occurring), and every individual is willing to mate with every other individual (no sexual selection either). Suppose you know how many of each allele is in a particular generation - the overall percentages of A and a. What will be their percentages (or “frequencies”) in the next generation?
That last is one of the key questions in the study of population genetics - how allele frequencies change from generation to generation in a given population. For the above imaginary population, the answer is called the Hardy-Weinberg equilibrium.
The Math
The Hardy-Weinberg equilibrium for two alleles at one locus is: p_2 : 2_pq : _q_2.
So what does that mean? First, p stands for the percentage of allele A in the population, and q stands for the percentage of allele a. Since the total number of alleles adds up to 100%, q is also 100% minus p. (More conventionally, these are usually written as decimals, so q = 1 - p.)
When two individuals in the population mate, there is a p% chance that the egg will have allele A, and a q% chance it will have a. Likewise for the sperm. The chance for an egg and sperm both with A will therefore be p x p, or p_2. Likewise for a and q. The chances for a match of A and a, or a and A, are p x q and q x p, which makes it 2_pq.
Thus, individuals of the next generation will have a p_2% chance of being AA, a 2_pq% chance of being Aa, and a _q_2% chance of being aa.
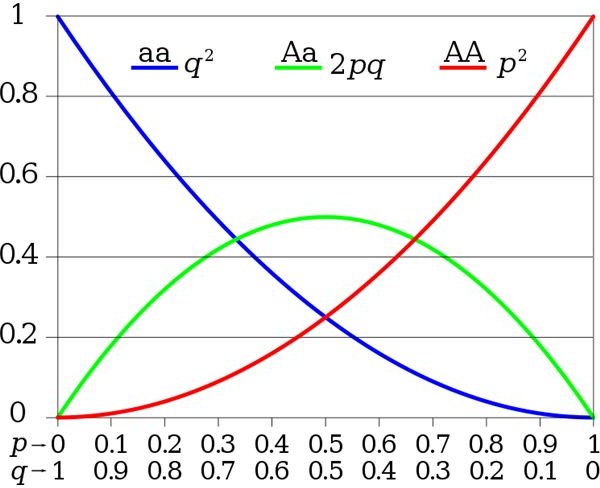
The Chart
So much for the basic math. Now look at the chart to the left, which shows the frequency diagram for every possible combination of A and a in the population. You read it by where the lines fall on the Y axis (the vertical bar). For example, when the population has 100% A, it has 0% a, and every individual will be AA. The Hardy-Weinberg equilibrium for the population is therefore 1 : 0 : 0. When it has 50% A, it also has 50% a - and the population will have 25% AA homozygotes, 50% Aa heterozygotes, and 25% aa homozygotes - or 0.25 : 0.5 : 0.25. You can find the frequencies for every other percentage of A or a in between as well. Just remember that the three numbers always add up to 1.
Once the alleles are in Hardy-Weinberg proportions, it stays exactly the same in all future generations - so long as mating remains random, no natural selection occurs, and the population remains large. Hence why it’s called an “equilibrium.”
Real Populations
So far we’ve been talking about an imaginary population. How do real populations violate Hardy-Weinberg principle conditions? Some examples:
- Populations can’t literally be infinite in size. The equilibrium still works, however, if the population is just very large. For small populations, genetic drift will eventually cause one of the alleles to be “fixed” while the other disappears, reaching a 1:0:0 equilibrium.
- Natural selection is often an important factor.
- Mating is not random for every gene in a real population - the phenotypes for some alleles will look more attractive to mates than others.
- There might be subpopulations that only mate with each other instead of with everyone in the entire population - for example, small groups on individual islands.
- There might be migration of new individuals into the population, which constantly brings in more of one allele than the other.
The Significance
So what’s the point of the Hardy-Weinberg equilibrium then? Basically it’s a comparison tool. If a real population’s frequency distribution doesn’t match the predictions of the theorem, it means something interesting is happening with that particular gene - which points us (population geneticists) in useful directions of research.
Hardy-Weinberg equations exist for other configurations of alleles and genes as well - for example, a gene with three alleles instead of two (the human ABO blood group system is a good example). Each configuration has its own set of frequency distributions. When there are two or more genes (two locuses), it starts being more about haplotypes than genotypes, and the analogous frequency equations are called linkage equilibriums.
References and Image Credit
Ridley, Mark. 1993. Evolution. Blackwell Scientific Publications, Inc.
Griffiths, Anthony J.F., Jeffrey H. Miller, David T. Suzuki, Richard C. Lewontin, and William M. Gelbart. 1993. An Introduction to Genetic Analysis 5th ed. W.H. Freeman and Company.
Diagram by Johnuniq, used under CC-A-SA 3.0 unported license.
This post is part of the series: Topics in Population Genetics
Population genetics is a study of the characteristics of genetic variation in populations of individuals, and how it changes with generation. These articles explain the basics.