How Fast Does the Earth Rotate?
Rotational Speed Versus Latitude
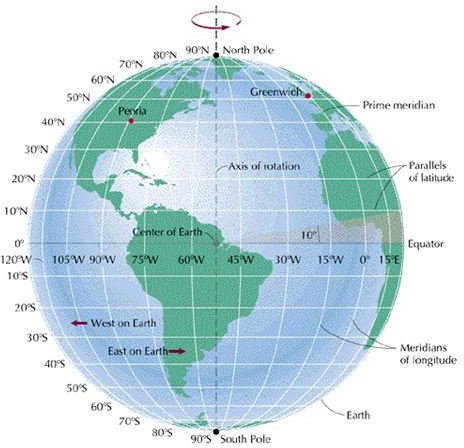
We know how long it takes the Earth to rotate around its axis; it takes 23.93 hours. The circumference of the Earth at the equator is 40,075 km (24,901 mi). So take 40,075/23.93 and the rotational speed is 1,675 km/hr or 1,040 mph. We also know that at different locations on Earth the circumference changes, so the rotational speed changes.
Here are the rotational speeds at different latitudes.
- At 80° - 289.9 km/hr (180.1 mph).
- At 70° - 571.1 km/hr (354.8 mph).
- At 60° - 834.9 km/hr (518.7 mph).
- At 50° - 1073.3 km/hr (666.9 mph).
- At 40° - 1279.1 km/hr (794.8 mph).
- At 30° - 1446.1 km/hr (898.5 mph).
- At 20° - 1569.1 km/hr (974.9 mph).
- At 10° - 1644.4 km/hr (1021.7 mph).
- At 0° - 1675 km/hr (1040 mph). (The Equator)
.
See Also: What is the Difference Between Rotation Period (Sidereal Day) and Planetary Day?
Rotational Speed and Space Launches
The rotational speed affects space launches. The escape velocity of a spacecraft to reach outer space is about 25,000 mph. By launching from the equator, or a nearby location, a space agency will be able to launch its vehicles using less fuel, or more cargo or supplies using the same amount of fuel. Cape Canaveral is 1967 miles from the equator. For comparison’s sake, that is the same distance from Cape Canaveral to Salt Lake City, Utah. While there are no space launch spots at the equator, that is why launching from Florida made more sense than launching from, say Michigan.
There is one site that is near to the equator. That is the Guiana Space Centre. It is a French space launch site near Kourou in French Guiana. It has been operational since 1968, and its location is 310 mi north of the equator, at a latitude of 5°10'.
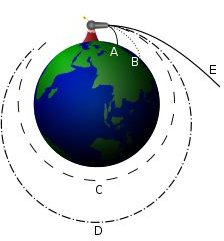
Isaac Newton’s analysis of escape velocity. Projectiles A and B fall back to earth. Projectile C achieves a circular orbit, D an elliptical one. Projectile E escapes.
If the Earth Rotates Why Don’t We Get Dizzy … and other Interesting Questions
Let’s start with the question of this section. We never get dizzy when the Earth rotates. Why Not? The answer is that we are spinning at the same rate that the Earth is spinning—relative to the speed of the Earth, the speed that we exhibit is zero (0).
That leads to another question. Why don’t we, and all other objects, just spin off the Earth and fly into space? The answer is that there are are two forces that are in play here - gravity in the form of a centripetal force and the inertia of the objects that are spinning.
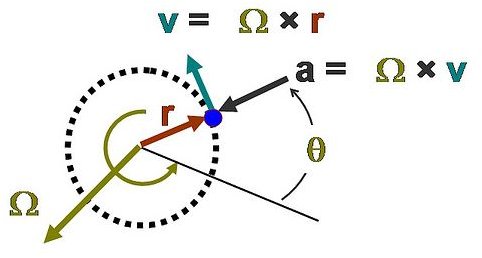
Explanation of the Image: The vector (or the magnitude and direction of an object ) represents the relationship for uniform circular motion. V is Velocity, r is radius. The vector Ω represents the rotation and is perpendicular to the plane of the orbit. So the velocity is given by a vector formula as V = Ω x r. Here is what that means.
Imagine that you tie a ball to a string, and you start spinning it around. One force wants to break away from the center and go off on its own; and the other is the force that keeps the ball attached to the center, which in this case is the string. If you let go of the string, the ball flies out.
Now because you are spinning around on the Earth, a similar force exists that wants to push you off into space. But, like the ball on the string, that inertial force is not very strong, and it is totally overwhelmed by the force of gravity (the string) that is keeping you attached to the Earth. The force that wants to throw you into space is only 0.3% of the force of gravity, whereas the centripetal force is 99.7%. So, people and things are going to stay put. They will not spin off into space.
Summary
The speed of the Earth’s rotation can be measured from different points on the planet, but the one most frequently taken is from the equator. There the circumference is 40,075 km (24,901 mi). The Earth day is 23.95 hours. Dividing the km/hr or mi/hr gives us a rotational speed of 1675 km/hr or 1040 mi/hr. That is the rotational speed of the Earth. One interesting fact is that the escape velocity to reach space is less at a point closer to the equator than at locations further away.
See Also: Jupiter’s Period of Rotation
References:
https://www.astronomytoday.com/
https://www.brighthub.com/science/space/articles/69733.aspx
Image#1 Credit: Montgomery College, https://www.montgomerycollege.edu/Departments/planet/M_AS102/coordinates/LatitudeLongitudeEarth.html
Image#2 Credit Wikipedia Commons, Escape Velocity, https://upload.wikimedia.org/wikipedia/commons/7/73/Newton_Cannon.svg
Image#3 Credit: Wikipedia Commons, Circular Motion, https://upload.wikimedia.org/wikipedia/commons/0/00/Circular_motion_vectors.PNG