Lagrangian Points, Three Body Systems, and Gravitational Stabiility
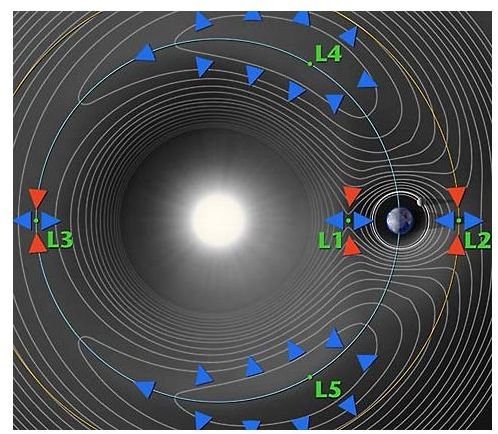
Where Are The Lagrangian Points?
An analogy: think of geostationary points orbiting Earth. A satellite in a geostationary orbit will forever be in orbit directly over the same point on the planet. The satellite, thus, appears to be “fixed” relative to Earth.
Lagrangian points are like this, except on a larger scale. Take a two-body system, with each body being large enough to exert significant gravitational influence on a third, smaller body. Within this system, there are five points where the opposing gravitational fields may hold this third body stationary relative to the other two bodies. These points are the Lagrangian points.
Points L1, L2 and L3 exist on a line drawn through the two large bodies, interspersed on each side and between them. These are the easiest to intuitively understand of the points.
Points L4 and L5 are a bit more complicated, existing at the third corner of two equilateral triangles that share the line drawn between the two bodies as a base. One triangle is drawn from the center of mass of each object, the other is drawn from the center of mass between the two bodies to the center of mass of the smaller body of the two, such that that third corner is closer to the smaller body than the larger body. These points are sometimes known as triangular Lagrange points due to this derivation, or as Trojan points, as the famous L-4 and L-5 points of the Sun-Jupiter system are named the Trojan Camp and the Greek Camp respectively.
This is all assuming that these bodies are orbiting each other on a single plane. Bring a third dimensions to the problem, and the solutions get very complicated very fast. However, we don’t need to worry about this with most actual orbits, as they exist upon a single plane.
Obviously, this is all tremendously complicated by the existence of other bodies in the universe. While their gravitational influence may be smaller, they make true Lagrangian points a technical impossibility. This influence may be great enough to entirely destabilize the point: the L3 point of the Sun-Earth point is a great example of this, as Venus’ orbit comes close enough to it that it is highly unstable. However, the influence is generally slight enough that these points may largely still be used for practical purposes.
The Geometry of Lagrangian Points
What Are Lagrangian Points Used For?
Lagrangian points have proven to be a stable place to put satellites. While it is difficult to place a satellite directly on the Lagrangian point, it is relatively easy to set it at an orbit around the point. Many of these are quite complicated, such as the Lissajous orbit. Missions utilizing the Lagrangian points are varied, from SOHO to the Herschel Space Observatory.
Each point has proven uniquely useful for observational purpose. For the Earth-Sun system, L1 is ideal for making observations of the Sun, with continuous sight of the Sun never being shadowed by either the Earth or the Moon. Conversely, L2 has proven to be excellent for observing celestial objects without influence from the Sun, it always being shaded by the Earth.
Lagrangian points in general are found sprinkled throughout science fiction literature, as hiding places for enemy starcraft, to clouds of breathable air around neutron stars, perfect points for space colonies to the best place for a view from your starship. The imagined uses for them are endless, and some of them are even being somewhat considered. The Earth-Moon L4 and L5 points, for instance, have been named as ideal places for space colonies, and a solar shade for influencing climate change would be placed at the Sun-Earth L1 if the idea ever gets off the ground.
For more information, Wikipedia has an excellent article on Lagrangian points, including the mathematics behind them, a list of missions that utilize Lagrangian points, an extensive list of references to Lagrangian points in science fiction literature, and more.