Planetary Motion - Ideas Before Kepler's Laws Were Conceived
Attempting to understand how the planets move has been an obsession of astronomers since people first began to look up at the stars. Indeed, the Greek philosopher, Thales, is said to have fallen into a well once because he was too busy looking up examining stars. They are a natural target of curiosity, so you can hardly blame him: hundreds of thousands of bright pricks of light, moving across the sky with the time of night and the season—and some made patterns that just didn’t make sense to astronomers, loop-to-loops and spirals in the sky. Eventually, Kepler came along and figured it all out, but he built upon centuries of work by countless other astronomers, just to figure out the basic structure of our solar system.
Pre-Kepler: Epicycles And Geocentricism
All those odd years ago, a theory called geocentrism existed, that the Earth is the center of the universe and that everything, including the sun, orbits it. This stemmed from the general human feeling that, of course, our species must be the center of it all; this was later expressed in statements in the Bible, which for centuries was taken as scientific truth.
Of course, the scientists had difficult reconciling canon with what they were observing. Over-elaborate models for planetary motion included some movements that today are most likely to be found on a roller coaster.
Eventually, with much resistance by the religious institutions of the day, geocentricism was overtaken by heliocentricism through the work of astronomers like Copernicus and Galileo. Though this theory simplified models of planetary motion considerably, it still didn’t explain a critical kink: a short backwards movement in the orbit of every planet - called retrograde motion, the usual forward motion being known as prograde. This was explained through an older Greek theory that called for epicyclic movement of the planets, or a short circle within the greater circle within the orbit like a loop-to-loop.
This was later to be unraveled to really just be another consequence of our perspective from here on Earth: since we are not, actually, at the center of the universe, nor even our solar system, we are observing the movement of the planets from a skewed angle.
However, serious problems still existed with the theories of planetary motion. Everything was assumed to move in circles, a belief that stemmed from the thought that celestial motion must be perfect, and thus in the clean smooth lines of a perfect circle.
It never really occurred to anyone that all those little discrepancies between observation and theory that they were still finding—planets moving too quickly here, or too slowly there—might be due to non-circular motion. Until Kepler, that is.
Deriving The Laws
Kepler did not have a computer to help him out. Let’s get that perfectly straight from the get go. Imagine doing this all by hand. Calculations made trivial by the modern convenience of the computer took hundreds or even thousands of hours for him to complete by hand with nothing but pen, paper, and his brain.
Nor did he derive his theories from preexisting notions. He took thousands of data points, observations of all the known planets, taken from himself and from astronomers such as Tycho Brahe, and just crunched the numbers. His laws are empirically derived, found to fit exactly what the data says is true.
Kepler’s Laws work not just for planetary motion, but for any object orbiting another, from moons orbiting their own planets to asteroids and comets. With a little geometric wizardry, one can even derive the laws for binary star orbits. The relative masses of the two objects, their distance between each other, none of it matters, as long as they are orbiting each other—ultimate generality, something all scientists yearn for when they attempt to explain things.
Indeed, later astronomers found that they perfectly agreed with even more general physical laws. Deriving Kepler’s laws from Newton’s own laws and basic geometry, in fact, is a staple assignment of many introductory level college physics courses. The enormity of his accomplishment, the originality and veracity of his claim, is one that must be admired.
Without further ado, Kepler’s Laws on the next page:
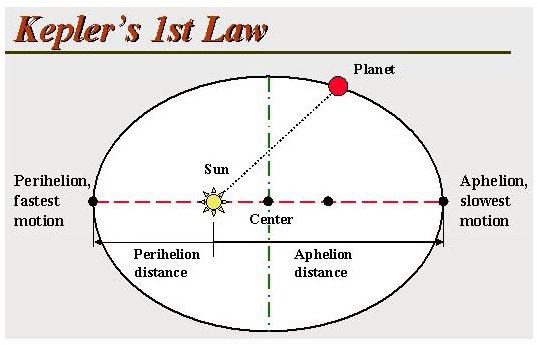
Law 1: The Orbit of Every Planet is an Ellipse with the Sun at a Focus
Take a trip back to those geometry classes. The mathematical definition of an ellipse involves having two focii, one at each side of the center of the ellipse in perfect symmetry. The object that is being orbited around must be at one of these focii, even if there is absolutely nothing at the other.
The amount of “ellipseness” in a given orbit as opposed to “circleness”, referred to as a planet’s eccentricity, varies tremendously between the planets. Some are nearly circular, such as Venus, while others are as dramatically elliptical as (the non-planet) Pluto’s. However, most planetary orbits appear to look very similar to circles, and given the relative crudeness of their observations, it’s startling that Kepler was even able to tell the difference between a circular orbit and an elliptical one with his data.
Kepler’s Laws In Action
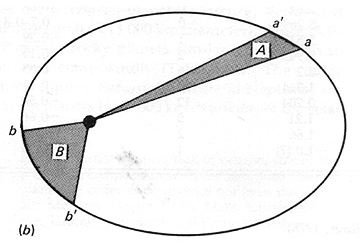
Law 2: A Line Joining a Planet and the Sun Sweeps Out Equal Areas During Equal Intervals of Time
This one might be slightly difficult to visualize. Make a mental line between the orbiting and the orbited, and then take an arbitrary amount of time and have the line move along. During this time along any interval of the orbit, the same amount of area should be swept out. The consequence of this law is that when the planet is closer to the sun, the planet will move faster, but if the planet is further away, it will move slower so it does not move as far along the orbit so that these two intervals will indeed sweep out the same amount of area.
Geometry whizzes will note that this is an obvious consequence of the First Law; indeed, all of Kepler’s Laws are really just restatements of each other after a little geometry. However, with this phrasing it is more obvious what Kepler’s Laws indicate as far as the kinetic and potential energy of the planets are—and thus how their velocity changes. This is important, because it explained the slight differences in speed that Kepler noted in the planets during different parts of their orbit.
Law 3: The Square of the Orbital Period of a Planet is Directly Proportional to the Semi-major Axis of its Orbit
Ouch!
Read that statement over a few times, and it’ll start to make sense. Mathematically, it can be simplified to: P2 is proportional to a3. As with the others, this law is just a restatement of the previous laws . The difference here is that it’s more mathematical, which may or may not make more sense. However, it’s very elegant, and has served countless astronomers well over the years in figuring out the distance to a variety of objects orbiting our sun.
That proportionality constant implied in the law is the same for any planet that orbits the same body—so, from Venus to Uranus, everything that orbits the sun, they all share that same constant. Using this, one may find the period or semi-major axis of an unknown object by using a known one in the same system, by comparing P2/a3 for each object.
What Kepler’s Laws Do Not Cover
Not everything works out perfectly, however: the universe has a lot of variables in it, and planetary motion is no exception. One of the biggest things effecting the accuracy of Kepler’s predictions is the gravitational pull that the planets exert on each other, which can cause subtle variations in orbit known as gravitational perturbations. In addition, the atmospheric drag of a planet as it hurtles through not-quite-empty space, collisions and other effects can cause small, but relevant changes to a planet’s orbit. These may all be taken into account, however, with today’s mathematical modeling of the universe. Thanks to Kepler and other astronomers, we finally have a complete understanding of how celestial objects move about each other.