Why a parabola has a perfect focus? - A Geometric proof

1. Parabola: It is the locus of points which are equidistant from a point (known as focus) and a line (known as directrix) in a specific plane. This particular definition of the parabola will be very useful in our proof. For the sake of completeness, the parabola is a conic section with the equation y² = 4ax in the simplest form.

2. Principle of least time: One of the very interesting properties of light, given by Fermat, is that the path taken by a light ray between two points is either minimal, maximal or an inflection point. Equivalently, the change in time taken by light due to infinitesimal changes in the path of light should tend to zero. Although, this was not the original form of Fermat's statement, this is usually stated as the modern form. A consequence of this is that - "If we can prove that light rays originating from a source take the same time to reach a point, then they will focus at that point".

Now, we can proceed with our actual proof.

To prove: A parabola will focus all rays coming from infinite, and parallel to its axis, to a single point which is its focus.

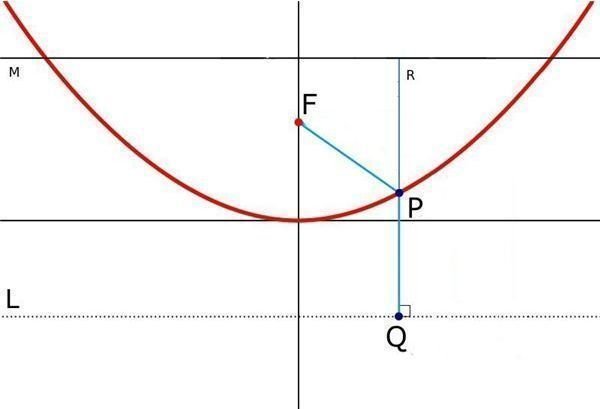
In the image to the left, the red line is the parabola, the point F is the focus and the line L is the directrix. Thus, every point on the red line is equidistant from F and L. The axis of this parabola is the vertical line.

Now, we need only prove that all rays coming parallel to the axis need to travel the same distance to reach F.

Let us consider another line M parallel to L. All rays parallel to the axis originating at the same time will reach line M at the same time. Thus, they will also reach L at the same time.

Now, notice that the length FP = PQ by the definition of parabola.

For any arbitrary ray,

Distance from M to L = RP + PQ = RP + FP.

So, if rays reach L at the same time, they must reach F also at the same time as the distance is same. Thus, all rays coming from infinite and parallel to the axis will focus at F.

Hence, proved.