Mathemematics and How It Relates to Astronomy & How Astronomers Use Math
How Mathematics Are Used In Astronomy
Kepler’s Laws of Planetary Motion taught mankind how the planets circled the Sun. This mathematical concept expanded on an observation that Copernicus originally made. It describes celestial mechanics or how the planets move through the Solar System in elliptical orbits. Describing how bodies move in relation to one another, and learning more about them is a core element of astronomy. It was left up to Newton’s Law to provide a useful gravitational relationship for space exploration. This is known as Newton’s Law of Universal Gravitation. The Newtonian law is basic to describing planetary escape velocities, orbital slingshot mechanics, and satellite fly-bys. In each scenario, astronomical information is being gathered, but mathematics makes it possible to these perform missions. It also allows us to interpret the information gathered.
Listed are Kepler’s First Law and Newton’s Law of Universal Gravitation:
Kepler’s Law:
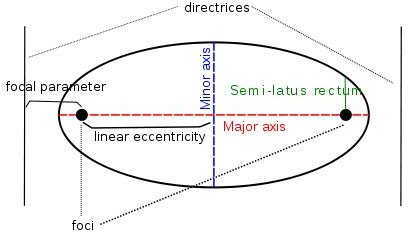
R = P/(1+eCOS (Θ))
**
Where R is the radius of the orbit, P is the semi-latus rectum, and e is the eccentricity.
*R and Theta are polar coordinates that predict where a planet is in an elliptical orbit.
Newton’s Law:
F = G(M1)(M2)/R2
Where G is the Gravitational Constant, M1 and M2 are the masses of concern and R is the distance between them.
*Force = Gravitation force
Please note that Kepler’s Laws of Planetary Motion were used to derive Newton’s Law of Universal Gravitation. Kepler’s Laws of Planetary Motion was published in 1609 and Newton’s Law of Universal Gravitation was written in 1687. Now let’s review the science of observation.
Other Applications for Mathematics
Radio telescopes provide information from the unseen electromagnetic spectrum. This includes infrared radiation, X-rays, gamma rays and cosmic radiation. Radio telescopes use complex equations to separate radio frequency “noise” from true deep space signals. This math-based process is known as filtering. Today, digital filtering techniques are used extensively to manipulate the data gathered from an observation, either to eliminate noise and/or enhance the desired frequencies from the object of study.
Calculating the redshift of a galaxy or distant heavenly body can be used to tell us whether it is moving toward our planet or away from it. This is accomplished using the famous redshift equation, which is listed below:
z = (λ(observed) - λ(emitted))/λ(emitted)
z - distinction between red and blue shift
λ - wavelength of light
The motion of the universe was a critical factor in developing the big bang theory. Knowing and understanding the redshift has provided a tremendous amount of information about how the universe was formed and its potential future.
Mathematics are the key tool that has made planetary exploration and astronomical interpretation possible. The only idea more appealing than knowing what is out there, is visiting the stars ourselves. When we do visit the stars, math will make that possible as well.
Historical Mathematical Techniques In Astronomy
Humans have been observing the stars long before the invention of the Hubble telescope and spectroscopy. Mathematical techniques have been used to perform complex calculations to predict eclipses and other heavenly events. In fact, many famous astronomers were also mathematicians. One of the core elements of studying the stars is spherical trigonometry. This mathematical science allows astronomers to project the spherical heavens onto a flat surface for mapping.
Some of the first tools for measuring heavenly positions came along when longitude and latitude were developed for calculating global positions relative to the Sun’s motion. Today we use these systems for measuring the position of any object on Earth. The most critical part to doing this calculation involved the use of a maritime clock called a chronometer. John Harrison and Edmund Halley were a principle contributors in this measuring tool.
Some of the greatest breakthroughs in mathematics came while trying to study the stars. Some of these include the invention of zero, solutions to triangulation problems, techniques for the measurement of angles and predictive tools for the Moon’s visibility. Most of the these techniques involve geometry, trigonometry and algebra. Mathematics enjoys a rich history in astronomy as the two disciplines are heavily intertwined.
Interestingly enough, several of the older trigonometric techniques for predicting planetary positions were made into tables for calculations. Kepler studied these tables and devised his laws of planetary motion from them. It is interesting how each scientist builds the future from past, one observation at a time. Mathematics is essentially the basis of ancient, middle age and modern astronomy.
References
List references that you used for the article here:
https://www.hps.cam.ac.uk/starry/mathematics.html
https://imagine.gsfc.nasa.gov/docs/teachers/lessons/xray_spectra/background-spectroscopy.html
https://edmall.gsfc.nasa.gov/2000invest/spectra2.html
https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion
https://en.wikipedia.org/wiki/Newton%27s_laws_of_motion