Wind Power Formula using Wind Speed and Windmill Efficiency
Wind Turbines and Power Generation
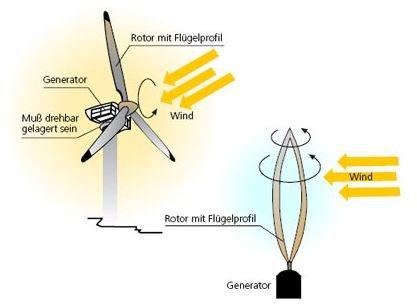
Wind turbines convert the kinetic energy of the wind into mechanical energy. On the top of the large turbines there’s a generator that converts the mechanical energy into electrical energy. Gears connect the generator to the turbine shaft and the electronic systems of the turbine regulate the motion in order to produce electric current of a specific frequency (60 Hertz or 50 Hertz depending on which country) and voltage.
Wind Turbine Efficiency

Efficiency is generally determined by the ratio of energy output to energy input. According to the Second Law of Thermodynamics, the efficiency of a device can never reach 100%; there is always some loss in energy and this applies to windmills too. For a wind turbine the energy input is the kinetic energy of the wind and the energy output is mechanical rotating energy.
Secondly, according to Betz’s law (1919), the wind turbine efficiency of converting the kinetic energy of the wind into mechanical rotating energy can never exceed 59%. This is the best possible conversion rate, as was proven by the physicist.
Efficiency is also determined by the design of the windmill. A given design has a peak efficiency at a certain wind speed. Below or above this specific speed value, the efficiency may stay the same or even drop down. For example, if a wind turbine has a top efficiency of 50% at a given wind speed of 10 meters per second, it will probably drop to 45% or lower if the wind velocity increases or decreases.
Another thing to keep in mind is that the generator converting mechanical to electrical energy, has a conversion efficiency as well, which is well below 100%. This fact lowers the overall efficiency of power conversion to a smaller value of 20-30%.
Formula for Calculating the Wind Power Produced
The formula used to calculate the wind power produced by a wind turbine or windmill is the following:
P = c x d x (D^2) x (v^3)
P: Power produced (mechanical) (Watts [W])
c: constant
d: density of wind (kilograms per cubic meter [kg/m^3])
D: turbine blade diameter (meter [m])
v: velocity of wind (meters per second [m/s^2])
The constant c depends on the system of units used and the specific variables in the equation. The formula implies that once the wind speed doubles, the wind power increases by a factor of eight! Furthermore, if the diameter of the blades is doubled, the power increases by a factor of four! The faster the wind and the bigger the blades, the more power input we can get.
In order for the formula to be more accurate, another variable should be added that is related to the design efficiency as mentioned above. This is the efficiency number of the wind turbine and it is provided by the manufacturer.
Sources:
- www.reuk.co.uk : Calculation of Wind Power
- www.ftexploring.com : Wind Turbines and the Energy in Wind
- www.provinz.bz.it
- https://www.gaia-mbh.de/windenergie/technik/
