Definition of Star Magnitude and How It Works: Measure of the Brightness a Star or Another Celestial Body

Definition of Star Magnitude and How It Works: Measure of the Brightness a Star or Another Celestial Body
Page content

Define Star Magnitude

Star magnitude is often associated with star brightness. In fact the first astronomer that classified stars was the Greek astronomer Hipparchus who classed stellar objects according to their brightness, where the brightest star had a “magnitude 1”, followed the next brightest “magnitude 2”, and so on until he reached “magnitude 6”, which was the faintest he could see. This makes the scale about 2000 years old.

The brightness of a star depends on the distance between the star and the observer. The brightness of a star is called the apparent magnitude, while the absolute magnitude of a star is a measure of its brightness as if it was 10 parsecs from Earth. (A parsec is 3.26 light years, so this would be 32.6 light years away.) This gives a common reference point to compare different stars and their brightness. Note that luminosity is a star’s intrinsic brightness measured across the electromagnetic spectrum, for the entire object, which is independent of distance.

There are two factors that affect apparent magnitude, how bright the star is, and how far away it is from the Earth.

The Pogson Scale

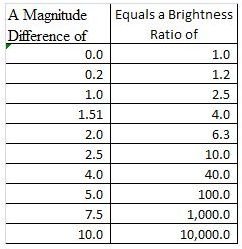
The Hipparchus scale had some flaws but astronomers kept parts of it. Now it is embellished with the Pogson scale. First formulated mathematically by N. R. Pogson in 1856, it says that one a magnitude integer in the scale is equal to 2.512. A difference of 5 magnitudes corresponds to a difference exactly 100 in the intensities of the stars. Thus a difference of 1 magnitude is the equivalent to taking the fifth root of 100, which is 2.512. Here is a table of how the magnitudes are related to brightness.

Now to see this in operation one can start with the Star Vega. It has a brightness magnitude of zero, or very close to it, 0.03, so this is the central point. The scale now reflects large negative numbers as well as large positive numbers. In the next table, one is able to see some well known objects with their apparent magnitudes displayed.

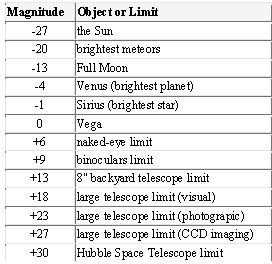
Magnitude Scale

It may be odd to think that the brightest object in the sky, the Sun, has a large negative magnitude value. But again, this is in part with astronomers keeping the original 1 to 6 scale of Hipparchus. On the other hand, the Hubble Space Telescope in searching for distant objects can pick them out with very small luminosity.

Absolute Magnitude and Distance

Once the apparent magnitude is known the absolute can be determined.

The absolute magnitude of an object is based on its parsec distance from Earth, i.e., 10 parsecs. In the table below, one can compare the apparent and absolute magnitudes of some stellar objects. The absolute magnitude determines the value of the intrinsic brightness of the star. This is important for astronomers to find because even if a star is very bright, it may be because of its nearness to Earth. It would not reflect its true luminosity. This moreover, is important in finding the distance to a star.

Here is a comparison of m (apparent magnitude) and M (absolute magitude) for five stars. If you know the apparent and absolute magnitude, you can determine its distance.

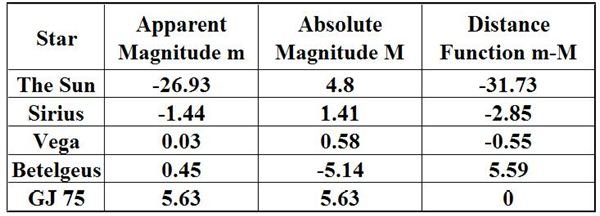
Absolute Magnitude

Here is what this table means:

  • The Distance function = m - M_._
  • If m-M is negative then the stars are closer than 10 parsecs.
  • If m-M is positive then the stars are further than 10 parsecs.
  • The size of the distance function determines the actual value of the distance, so that a star of distance function 1.5 is closer than one with a distance function of 8.7.

The formula to determine the parsec distance is: m - M = 5 log(d/10) where d is in parsecs.

Let us look at some of the elements of the table. First, just exactly how far away is GJ 75? Notice that the apparent and absolute magnitudes are the same. Why? Simply this: the star is actually 10 parsecs away from earth, so by definition its two, m and M, magnitudes must be the same.

Now look at Sirius. Its absolute magnitude is higher, and consequently dimmer, than its apparent magnitude. This means that distance wise it is closer than 10 parsecs to Earth. Betelgeuse’s apparent magnitude is higher than its absolute magnitude so it would appear even brighter in the night sky if it were only 10 parsecs away.

Bolometric Magnitude

There is another magnitude value that can be used. Stars have apparent and absolute magnitude. This is measured by visible light, one form of electromagnetic energy, but that is not all the energy that is radiated from the star. Stars will radiate energy across the entire electromagnetic spectrum from long wavelength radio waves to visible light to ultra short wavelength gamma rays. These other energy sources contribute to the energy output of the star, its luminosity. The Bolometric magnitude is the magnitude of a star’s energy measured across all wavelengths; it takes into account the total amount of energy radiated. This becomes more important as distances need to be computed with more accuracy. The absolute bolometric magnitude of a star measures its total energy emission per second

To find the bolometric magnitude a bolometer is used. It detects all of the wavelengths but it is most frequently used with wavelengths in the long wave-infrared (8 to 12, or 7 to 14 micrometers: the atmospheric window that is passes infrared light relatively unattenuated) range and microwave (30-centimeter to one-millimeter wavelengths). It is designed with a blackened surface so that the incoming radiation raises its temperature; this is measured using a change in electrical resistance.

The apparent and absolute magnitude of a star give astronomers a way of comparing stars for brightness, even if one looks very bright and another looks very dim. The very dim star may be more luminous if its absolute magnitude is greater than the star with a very bright apparent magnitude. You can also use the apparent and absolute magnitude of a star to compute the distance of the star in parsecs. Finally, the bolometer can be used to compute the bolometric magnitude which uses all wavelengths of a star, not just the visible wavelength.

References

The Universe Adventure https://www.universeadventure.org/fundamentals/light-magnitude.htm

The BGSU Project: https://physics.bgsu.edu/~layden/VarStarProj/vsp_extras.html

Ask An Astronomer: https://curious.astro.cornell.edu/question.php?number=569

Magnitude System: https://www.astronomynotes.com/starprop/s4.htm

Physics Lab: https://74.125.95.132/custom?q=cache:ARB8ZZK1CVAJ:www.physicslabs.umb.edu/Physics/Gelman/Gelmanfall06BrightnessandDistance.doc+difference+between+brightness+and+luminosity&cd=8&hl=en&ct=clnk&gl=us&client=pub-1415334591037307