Calculus and Astronomy: How do they Relate?
An Essential Element
Calculus is the mathematical language that describes change. One of the most common uses of calculus is to find the rate at which the position of a moving body changes with time. The laws of planetary motion that are commonly used by astronomers to calculate orbits are derived using calculus. An astronomer who wants to send a rocket into space uses calculus to work out how much fuel the rocket needs to accelerate to the correct velocity. These are just some examples of the ways in which calculus and astronomy work together.
How to Bring Your Rocket Up to Speed
Space travel is extremely important to astronomy. Space-based telescopes and probes, which collect huge amounts of information about the Solar System and beyond, are launched into space using powerful rockets. The rockets accelerate the spacecraft until it is going fast enough to leave the Earth’s gravitational pull and set off on its journey. Once the spacecraft is in space, the rocket thrusters are used to control its speed and direction.
A rocket burns fuel in a combustion chamber to produce exhaust gases. The pressure in the combustion chamber builds up so that the exhaust gases are forced out of the back of the rocket. The momentum of the gas traveling backwards causes an increase in the forwards momentum of the rocket due to the law of conservation of momentum.
How Much Fuel does the Rocket Require?
Astronomers who want to send rockets into space need to exactly know how much fuel is required to accelerate the rocket to the desired velocity. This can be worked out using calculus.
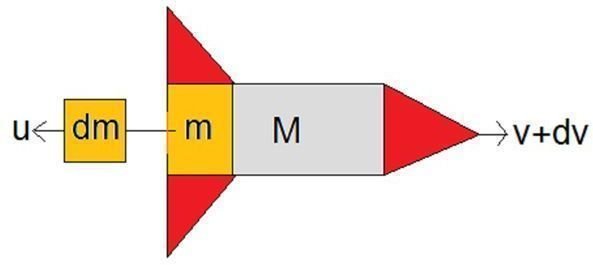
Our example rocket has a mass of M kilograms and carries m0 kilos of fuel. As the fuel burns, it produces an equal mass of gas, which shoots out of the back of the rocket, causing the rocket to accelerate. But what velocity will the rocket reach once all the fuel has been used up?
The principle of calculus is to consider a large change - the burning of all the rocket’s fuel - as the sum of lots of small changes. Consider burning a small quantity of fuel, of mass dm. The gas produced by the burning shoots out of the back of the rocket at velocity u. The momentum of the gas is given by its mass (dm) times its velocity (u).
Change in momentum of gas when it is expelled = u dm
Before the gas was expelled, the rocket was travelling at velocity v. The thrust from the gas causes it to accelerate, increasing its velocity by an amount dv. The total mass of the rocket, including the fuel that still remains in the tank, is (M+m).
Change in momentum of rocket = (M+m) dv
By the law of momentum conservation, the change in momentum of the rocket is equal to the change in momentum of the gas. That means we can combine the two previous equations to relate the tiny amount of fuel that was burned, dm, to the resulting increase in velocity, dv.
u dm = (M+m) dv
The increase in velocity that comes from burning all the fuel can be worked out by summing all of the small increases, remembering to adjust the value of m at each stage as the mass of unburned fuel that remains on the rocket decreases. The more steps that you split the total change into, the more accurate the answer will be.
This is where the real power of calculus comes in: it allows a completely accurate answer to be worked out. Calculus splits the total mass of fuel into infinitely small parts, so that the value of m changes continuously between each step. The sum can then be written as an integral.
Total increase in velocity = ∫ dv = u ∫ dm/(m+M)
This expression means “sum up all the terms, dm/(m+M), for values of m between m0 and 0.” When evaluated, the result is
Increase in velocity = u log(1 + m0/M)
The astronomers can now use this formula to work out how much fuel the rocket needs to accelerate to the correct velocity.
Kepler’s Laws of Planetary Motion
Kepler’s laws of planetary motion are some of the most important laws in astronomy. They describe the orbit of a planet around a star.
Kepler’s Laws
- Every planet follows an elliptical orbit around the star, with the star at one of the two foci of the ellipse.
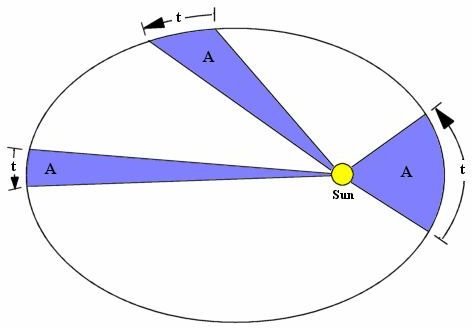
- The planet sweeps out equal areas of its orbit in equal time.
- The semi-major axis of the orbit (half of the longest diameter of the ellipse), cubed, is proportional to the period of the orbit (the time the planet takes to completely orbit the star once), squared.
Johannes Kepler worked out these laws by observing the motions of the planets. However, they can also be derived, using calculus, from Newton’s second law of motion (force = mass x acceleration) and Newton’s law of gravity.
Sources
Integrals: https://mathworld.wolfram.com/Integral.html
Rocket propulsion: https://hyperphysics.phy-astr.gsu.edu/hbase/rocket.html
Derivation of Kepler’s Laws: https://www.gaussianmath.com/calculus/keplerone/keplerone.html
Image credits
Rocket: created by author
Planet sweeping out areas: https://commons.wikimedia.org/wiki/File:Kepler2.gif