How does GPS Work?

Written by: Tolga BALCI • Edited by: Lamar Stonecypher
Updated Mar 4, 2010 • Related Guides: GPS Devices

What has thirty-one continuously broadcasting atomic-clock-equipped satellites orbiting the earth? What piece of inexpensive consumer gear listens for the signals and determines location based on triangulation and timing between the satellites? Here we'll look at the basics of how GPS works.

GPS Satellites

click to enlarge

The Global Positioning System is not a simple system. Inside the system are many different technologies that all combine and work together to allow one to find one's position on the earth, the sea, or in the air. The Global Position System depends on a number of GPS satellites (currently there are 31) orbiting the Earth. Each of these satellites continuously transmits the following information:

the time the information is sent,
exact orbit information
rough orbits of all GPS satellites
general system health

The time information here may seem to be the “easiest” part, but in fact it is just the opposite. There are atomic clocks inside the satellites which operate with a precision of one billionth of a second. The reason for this is that electromagnetic waves travel very close to the speed of light, which is about 299,792,458 meters per second or about 186,282.397 miles per second. So, if the atomic clock makes an error of 1/3300 of a second, then you are somewhere in a circle with a radius of 1000 meters. If we expand this further, an error of 0.13 seconds will place you “somewhere on Earth” because the electromagnetic waves travel the distance equal to the equator in 0.13 seconds.

Image courtesy of Coleparmer.

GPS Receivers: Determining Location by Trilateration

The signals transmitted by the GPS satellites travel freely in the space and in the atmosphere and reach our devices, which are called GPS receivers. The receiver, upon receiving information from the satellites computes the distance to each satellite. This method is called trilateration.

Let’s stop at this point and think about the trilateration issue: if you consider the satellite as a point which transmits the data to all directions, the transmission takes a spherical shape. If you slice the spherical shape, where one point is the satellite and the other is the Earth, you will have a circular shape. If you intersect more than one circle, then you will have an area. If you continue intersecting more circles, then the area becomes very small.

Trilateration Intersection of two circles

click to enlarge

In the image on the left, you see two circles. Imagine the circles as the signals from the GPS satellites. In this setup, you are basically somewhere in the yellow area.

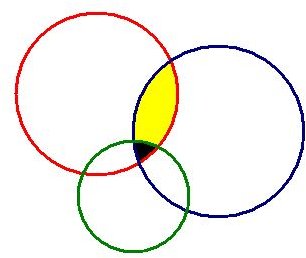
Trilateration Intersection of three circles

click to enlarge

In the image on the right, there are three circles. Note that all the circles’ radii are different. But the addition of the third circle significantly reduced the size of the area, which is the black area.

Combine these with the trilateration (or maybe quadlateration, pentalateration or more) and you will end up with smaller areas. This is the case with the Global Positioning System: the more satellites you see, the more precise is your location.

How Many GPS Satellites does My Device have to See?

Logic says that three satellites should be enough to give a good position. Considering also the space is three dimensional, the location can be calculated by solving the equations for three unknown parameters: Latitude, Longitude and Elevation. Is this really fine? Yes and no. If you input your elevation to your GPS receiver, then three satellites will be enough. However, you will still have to correct the time factor. The best way to do is to wait for a little time and let your GPS receiver “see” four or more satellites. With four or more satellites, and with the elevation you input, your location will be as precise as possible. But there is a very small basic fact: The GPS receiver’s antenna must look directly to the sky. You cannot run a GPS inside the house or in a closed place. The antenna must gather the signals without any interruption.

GPS Receivers: Derived Information

click to enlarge

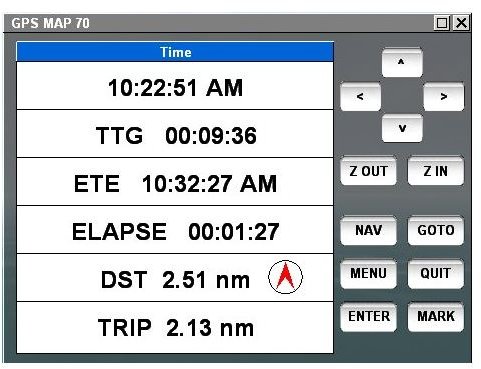
GPS receivers can also produce information derived from its computations like speed, course, distance etc.. This is fairly easy for the device: if you record position A, position B and the time spent between them, then it is easy to calculate the distance, the position of B compared to A and the speed. All that is done is solving some basic algebraic equations in analytic geometry.