What is Force Resolution, Polygon Law of Forces, and Triangle Law of Forces?

Resolution of force may involve the splitting of a force into many of its parts, without altering its influences on the body. Generally, the resolution of force is carried out along two mutually perpendicular paths.

Principle of Resolution

**

It states – “The algebraic sum of the resolved components of a number of forces, through a given path, is equal to their resultant resolved part in the same direction.”

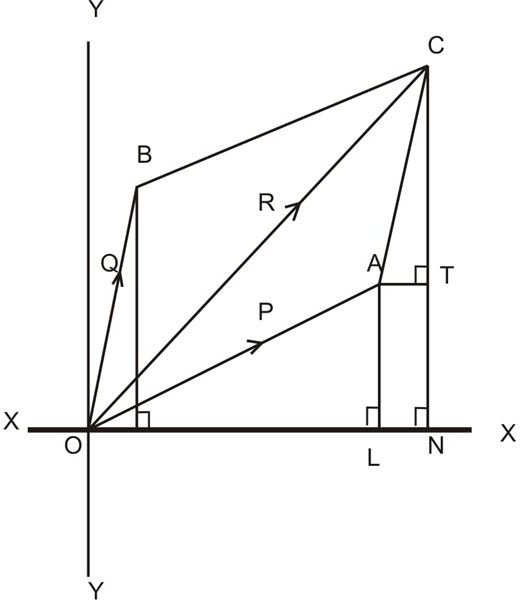
Referring to the figure, consider a couple of forces denoted as P and Q. Let the forces be represented in magnitude and direction through the sides OA and OB of the shown parallelogram respectively.

Here, it’s known that the diagonal OC represents the resultant of the two forces P and Q in magnitude and direction.

Let OX represent the direction needed for resolving the forces.

Drawing from the points A, B and C on OX, perpendicular lines AL, BM and CN, also from point A another perpendicular line AT on CN, we get two triangles OBM and ACT.

The two sides AC and OB are same in magnitude and are parallel. Also, OM is parallel to AT.

Therefore, OM = AT = LN.

The geometry of the drawing suggests, ON = OL + LN = OL + OM, since LN = OM.

However, ON is the part that’s resolved of the resultant R.

Similarly OL is the part resolved of P and OM of the force Q.

Therefore, finally we get the resolved part of OX and R = Resolved part of P along OX + Resolved part of Q along OX.

In the above example, for the sake of easier understanding, we took just a couple of forces; however the concept may be applied for any number of forces.

The magnitude and the direction of the resultant of the forces may be determined by:

• Analytical Method
• Graphical Method

Analytical Method – The following points identifies how the resultant force may be calculated using the analytical method:

Resolve the given forces vertically and calculate the algebraic total of all the vertical parts or Σ V.

Resolve the given forces horizontally and calculate the algebraic total of all the horizontal parts or Σ H.

The resultant force R of all the given forces can be expressed as:

R = (Σ V)^2 + (√ H)^2

The inclination of the above resultant force will be at an angle Ɵ with the horizontal component and may be expressed as:

tan Ɵ = √ΣV / √ΣH

For a given system of forces, the resultant may be identified graphically through any of the following methods:

• By Triangle Law of Forces,
• By Polygon Law of Forces,
• By the Vector Method

Triangle Law of Forces

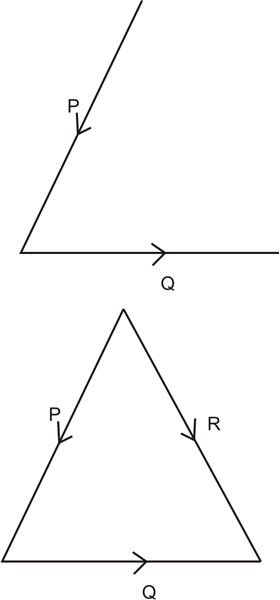
It states – “If a couple of forces applying simultaneously on a particle is represented in direction and magnitude taken in order by the two sides of a triangle, then their resultant can be represented in direction and magnitude by the third side of the triangle, taken in the reverse direction.

Consider two forces P and Q (see fig) acting over a common point, then by closing the remaining side of the triangle we get the resultant of the forces as R, with opposite orders.

Polygon Law of Forces

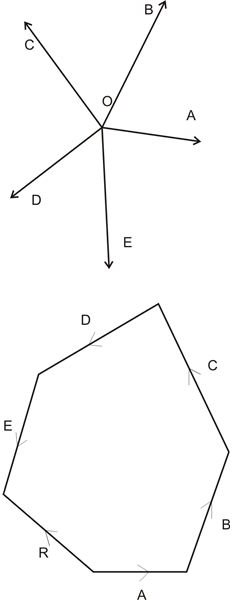
It states – “If several different forces applying simultaneously over a particle be represented in the order of direction and magnitude by the sides of the polygon, then the resultant of the entire forces can be represented in the opposite order of direction and magnitude by the closing side of the polygon.”

The figure illustrates five forces A, B, C, D and E, with arrows indicating their directions. The next figure provides the resultant of the five forces by R, which is the closing side of the polygon, but in the opposite direction, again shown by the arrowheads.

Vector Method of Calculating Resultant Force

The vector method provides an alternative method of calculating resultant force graphically, using polygon law of forces.

The following points explain how the resultant in magnitude and the direction of a given number of forces may be calculated by the method of vectors with the help of the shown figures:

• Draw the space diagram for the given forces.
• Next, choose an appropriate location and continue adding the forces vectorially with regard to the directions of the forces.
• Then the sides of the polygon which closes the figure, taken in the opposite direction to its adjoining forces, gives the direction and the magnitude (as per the scale) of the resultant of the forces.

References

Images - Drawn By the Writer

Book - Engineering Mechanics, By Bhavikatti, S.S - https://books.google.co.in/books

Tanstutor.com - https://www.transtutors.com/math-homework-help/Statics-And-Dynamics/triangle-law-of-forces.aspx