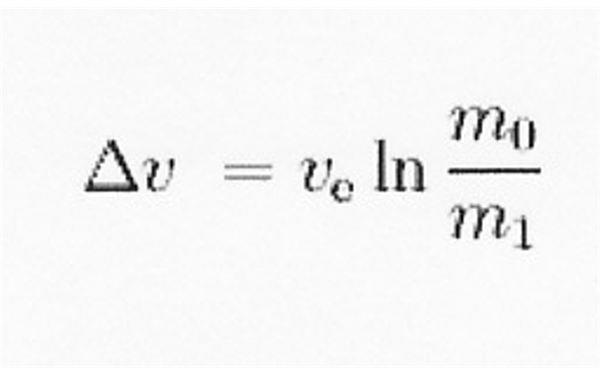Rocket Science Basics: Understanding Mass Ratio and Exhaust Velocity
Mass Ratio and Exhaust Velocity
The most basic factors in rocket science are the exhaust velocity (EV) of the propellants and the mass ratio (MR) of the vehicle. Various propellant combinations have differing exhaust velocities. The most common propellant combinations used today are LOX/RP-1 (Liquid Oxygen/Kerosene) and LOX/ LH2 (Liquid Oxygen/Liquid Hydrogen) as used in the Space Shuttle. These two have significantly different exhaust velocities. LOX/RP-1’s EV is about 7400 mph. LOX/LH2’s EV is 15000 mph.
Now of course a spacecraft must achieve a velocity of 17,500 mph to go into orbit. Not even LOX/LH2 could do that except for a unique physical phenomenon that allows a rocket to exceed the velocity of its exhaust if its empty weight at engine shutdown is sufficiently lower than its fully fueled weight at liftoff. That is its MR.
The basic MR equations were derived in 1903 by Konstantin Tsiolkovsky, who is revered in Russia as the Father of Russian rocketry. His equation is:
where:
m0 is the initial total mass, including propellant, in kg (or lb)
m1 is the final total mass in kg (or lb)
ln is the natural logarithm e (2.7183)
vc is the effective exhaust velocity in m/s or (ft/s)
Δv is the change in velocity you desire in m/s (or ft/s) (for low Earth orbit [LEO], it would be about 25,000 ft/s).
Note that Tsiolkovsky approached this from the stand point of achieving a predetermined velocity. To determine what MR gives you the desired velocity, rewrite the equation as follows:
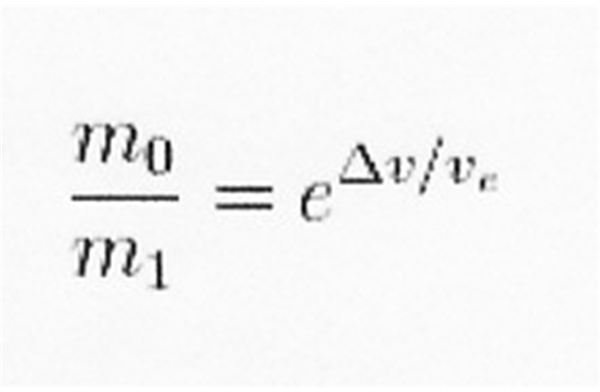
This equation indicates that a Δv of n times the exhaust velocity requires a mass ratio of en. For example, for a vehicle to achieve a Δv of 2.5 times its exhaust velocity, it must have a MR of e2.5 (approximately 12.2). The equation indicates that a “velocity ratio” of n requires a mass ratio of en.
Several years later, an American, Robert H. Goddard, wrote a treatise titled “A Method of Reaching Extreme Altitudes.” In this he expanded on Tsiolkovsky’s work and proposed using liquid fueled rockets to reach the moon. Goddard came to be known as the Father of American Rocketry, and built and flew the world’s first liquid fueled rocket. Later, after WWII, he would design and develop a high altitude research rocket for the Army—the WAC Corporal—that would play a seminal part in the beginnings of the U.S. ICBM and space programs.
Theoretically, a rocket can achieve its exhaust velocity if its mass ratio is e—the natural logarithm 2.7183. However, basic physics makes that impossible. A rocket must fight air resistance on its first minute or two of flight, and gravity all the way to orbit. The reality of rocket science is that the MR must be near 3 to achieve exhaust velocity.
The original “big” rocket, the German V-2, which used LOX and the equivalent of RP-1, had a MR of just over 3. It was small by today’s standards, however, standing just 50 feet tall, so carried a limited propellant load. Its burn time was just about one minute. Its velocity at burnout was about 3000 mph.
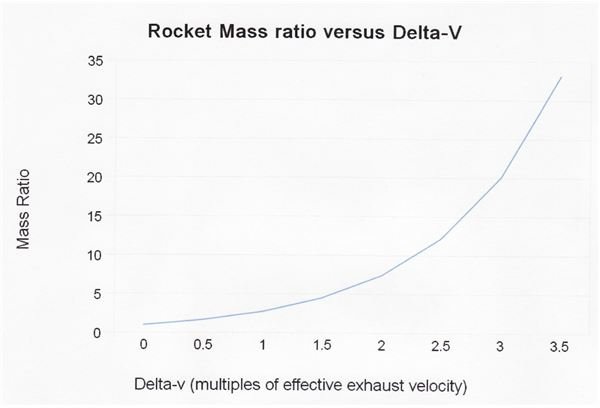
It was a single stage rocket. Still, if a rocket’s MR is more than 3, it can exceed its EV. The Mercury/Atlas vehicle that orbited our first astronauts had a MR of 12.3. Even with the relatively low EV of its LOX/RP-1 propellant, that was sufficient for it to achieve orbital velocity. Unfortunately, it isn’t a matter of the MR multiplying the EV. The Atlas’ MR was four times that required to match its propellants EV, but its maximum possible velocity was not four times its EV. That’s because when EV is plotted against MR it generates an asymptotic curve, as shown in the illustration. This is a curve that comes ever closer to a line or point but never touches it—even if drawn to infinity. You can see the Atlas’ MR—12.3–barely gave it a delta v sufficient to reach LEO.
Tricks of the Trade
Rocket scientists have a number of tricks up their sleeves to help put spacecraft in orbit or send them to the moon or interplanetary space. It’s no accident that America’s spaceport is located at Cape Canaveral. Oh yes, it’s a safe launch site, the rockets are launched over water, no populated areas are at risk. But those are pluses.
If you are a regular on the Space Channel, you know the Earth rotates on its axis at about 1000 mph. If a rocket is launched in the direction of the rotation, it picks up that velocity as soon as it leaves the launch pad. That’s 1000 mph the propellant doesn’t have to provide.
The rocket gets the full boost from Mother Earth only if it’s launched from or near the Equator, as are some of the European Union space ventures. From the Cape, the rockets are launched towards the Equator, and pick up a portion of that speed, enough to help them along.
Another trick rocket scientists have is the flight path, or trajectory of the rocket. Space rockets do not climb straight up into orbit. In the first place, they would be struggling far too much against gravity. Secondly, they would not go into orbit, but would continue to coast into space, slowing as gravity won out, until they came to a stop and began falling back to a fiery reentry. Orbiting spacecraft move across the planet horizontally. They must enter orbit that way. So the launch vehicles begin a pitchover program fairly early in the flight, so by the time the the spacecraft achieves orbital altitude it is ‘flying’ almost horizontally.
The very first two launches from the Cape were in the early ‘50s, before any launch pads were built. They were made to test two theories. One was that a vehicle could fly horizontally. The tests were called Project Bumper. It used a V-2 as a booster with Goddard’s WAC Corporal atop it. The vehicle pitched over and flew horizontally with no problem, to the delight of the scientists and engineers.

Twenty seconds into the Space Shuttle’s flight, it begins a pitch program that puts it at an angle of 78 degrees after 60 seconds. At that time it is experiencing maximum atmospheric pressure, known as Max Q. The spaceship continues its pitch-over maneuver once through MAX Q, so that by the time it achieves orbital altitude it is ‘flying’ horizontal to the surface of the Earth.
A spaceship can not pitch into a completely horizontal trajectory when there is even a wisp of atmosphere because the atmospheric drag would slow it down.
The other theory Project Bumper tested was the rocket scientist’s biggest trick—multistaging.
Staging the Way to Space
The Atlas achieved its relatively high MR with a very light weight structure—its integral tankage was virtually an aluminum balloon held erect by the propellants in it. It was almost a single stage to orbit (SSTO) vehicle, dropping off only its booster engines at burnout.
But Tsiolkovsky’s equations indicate that if a second stage is added atop the booster stage, the mass ratios of the two stages combine algebraically. What happens is that the upper stages become the payload for the lower stage. When the lower stage drops away, its entire mass is now gone from the equation, and the upper stage proceeds with its own MR. The equations for this are far too extensive for this treatment, but can be found in the credits. In the illustration below, the subscript p is for propellant mass and L is for payload.
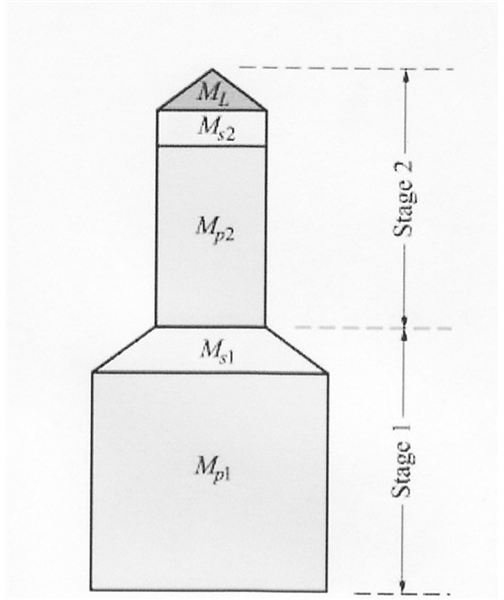
The SATURN V moon rocket was a three stage vehicle. Each stage had its own MR as it was ignited. The SATURN V’s overall MR was 23.1. The equations show there is an ideal arrangement for a three stage vehicle. The two upper stages should be 2/3rds the mass of the first stage. The third stage should be 1/3 the mass of the two lower stages. The Shuttle’s MR, a two stage vehicle, is 15.4. You can see from the graph on page 1 the multiple of the Shuttle’s LOX/LH2 propellant EV it can achieve, and why SATURN V’s upper stages were the same propellant.

Of course, the Shuttle’s main engines are ignited on the ground, so that high energy combination is propelling the spaceship ever faster into space from the time it leaves the pad. But why the solid boosters (SRBs), which have an EV of only 230? And why did the moon rocket use relatively low EV LOX/RP-1 in its first stage?
At liftoff, the main purpose is to lift the entire mass of the vehicle off the pad and get it started on its journey to space. This takes more than a high EV. It takes massive power. The SATURN V weighed 6 million pounds at liftoff. The shuttle weighs 4.5 million pounds. It took 7.5 million lbs of thrust to get the moon rocket on its way. Its liftoff was slow and stately. The shuttle, with its sold boosters, jumps off the pad with 7.8 million pounds of thrust. In both cases, all that was wanted was to get the upper stages to a reasonably high altitude–28 miles for the shuttle–and 3000 mph. Then the high EV engines can take over and propel the rest of the vehicle to its destination.

So these are the very basics of rocket science. In the next installment, we will delve into more advanced concepts, and look at how rocket engines create so much power.
Credits
Robert Goddard: NASA http://www.nasa.gov/centers/goddard/images/content/296776main_goddardchalkboard_HI.jpg
MR/EV graph: Wikipedia https://en.wikipedia.org/wiki/Rocket_equation
Bumper launch: NASA archives
Two stage rocket diagram: Georgia Tech https://www.ae.gatech.edu/people/ejohnson/ae1350-Fall2007/13.rockets.pdf
Two stage vehicle: https://www.apolloarchive.com/apollo_gallery.html
Shuttle launch: NASA https://www.nasa.gov/mission_pages/shuttle/multimedia/launch_gallery.html
References
- Personal knowledge
- Georgia Tech http://www.ae.gatech.edu/people/ejohnson/ae1350-Fall2007/13.rockets.pdf
This post is part of the series: Rocket Science–Just What is it?
Rocket science is a combination of physics and chemistry, with a smattering of aerodynamics, a bit of thermodynamics and mechanical engineering and orbital mechanics thrown in. It is a true interdisciplinary science.