How Do Interest Rate Term Structures Affect the Value of an Investment?
Whenever money is borrowed, more money is paid back than was borrowed. This extra amount paid back is expressed as an interest rate percentage. Interest rates represent more than just the amount over the principle amount borrowed that must be paid back to a creditor. They represent the risk associated with loaning the money.
The maturity of a loan is the amount of time that will pass before the loan is completely paid back to a creditor. Maturities in financial markets range from as little as a few hours to as much as thirty or even a hundred years. Banks often borrow money from the federal funds market for less than a day or overnight while some bond issues from corporations and government entities have maturities that span multiple decades. The majority of loans fall in between these extremes with the typical loan ranging from one to ten years.
Interest Rates and Maturity
There is a relationship between interest rates and maturity that becomes an important consideration for investors, both borrowers and lenders. For any class of loan such as a U.S. Treasury Bill, the relationship between the interest rate and the maturity is called the yield curve. The yield curve is nothing more than a visual representation of the interest rates for different maturities. There is one yield curve that is special in that it represents the relationship between interest rates and maturity for zero-coupon Treasury securities. A zero-coupon security is an asset that makes no payments during the life of the investment. Instead, the asset trades for less than its face value or at a discount and pays the full face value at maturity. For example, a $10,000 Treasury security may be initially sold for $7,000. As the security reaches maturity, its value rises closer and closer to its face value of $10,000 until the maturity date when it is worth exactly $10,000.
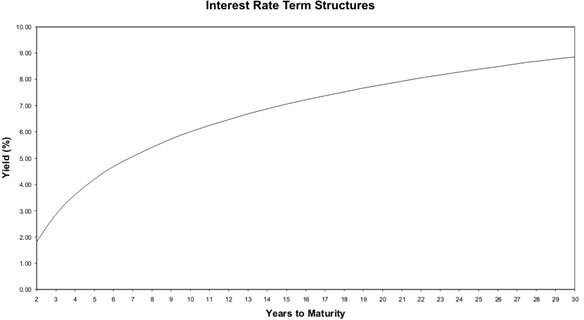
Figure
The Term Structure of Interest Rates
The yield curve for zero-coupon security is called the term structure of interest rates. This curve accelerates quickly for securities with short maturity dates but flattens out as the number of years until maturity increases. See the figure for a graph of a term structure of interest rate security yield curve. Risk of default and the tax status of securities affect interest rates. In fact, all things being equal, the interest rate associated with a security is a measure of the investment’s risk. Investments that take a long time to realize a return are riskier than shorter investments. Consequently, the interest rate for a longer investment, an investment with a longer maturity, is riskier and requires a higher interest rate. However, because of the time value of money principle, future cash flows contribute less to the present value of an investment than do sooner cash flows. Therefore, the risk of losing cash flows far into the future are less risky than a chance of losing cash flows expected in the nearer future. This is why the term structure of interest rates yield curve flattens out as the maturity of the asset increases.
Conclusion
The term structure of interest rates is a lesson in the relationship between risk and return. Longer maturities mean riskier investments and interest rates, a measure of required return, increases to account for the increased risk. Since cash flows far into the future contribute little to the present value of an asset, interest rates flatten out as the maturity of an asset increases. Notice that in the figure, interest rates increase as maturity increases over the entire graph but at a lesser rate for longer maturity assets than shorter maturity assets.